Mocninová funkcia

Šablóna:Dobrý článok Mocninová funkcia je typ elementárnej matematickej funkcie jednej premennej, v ktorej vystupuje len jeden člen s mocninou. Mocninová funkcia je špeciálnym prípadom polynomickej funkcie. Najznámejším príkladom mocninovej funkcie je špeciálny prípad kvadratickej funkcie. Podľa stupňa mocniny premennej sa rozlišujú mocninové funkcie rôznych druhov. V začiatkoch budovania matematickej teórie o funkciách boli predmetom skúmania práve mocninové funkcie, z ktorých bolo odvodené množstvo vlastností a vzťahov. K mocninovým funkciám sa neskôr pridružili aj ďalšie funkcie a spolu vytvorili skupinu pod názvom elementárne funkcie. Pomocou základných mocninových funkcií je možné modelovať veľmi veľa jednoduchých situácii a javov. Svoje opodstatnenie našli v samotnej matematike, vo fyzike, ekonómii a v mnohých ďalších oblastiach.

Krajne asymetrickým rozdelením/rozložením sa zaoberal napr. český geograf, demograf a štatistik Jaromír Korčák v dielach Deux types fondamentaux de distribution statistique (1938) alebo Přírodní dualita statistického rozložení (1941).

Definícia

Nech $a \in ℝ, n \in ℝ - {0}$ . Potom predpis

$f : ℝ \mapsto ℝ; x \mapsto f (x) = n \cdot x^{a}$

nazývame mocninová funkcia s reálnym mocniteľom. Ak $a \in ℤ^{-}$ potom ide o mocninovú funkciu so záporným celočíselným mocniteľom. Ak $a \in ℤ^{+}$ ide o mocninovú funkciu s kladným celočíselným mocniteľom alebo s prirodzeným mocniteľom.

Druhy mocninových funkcií

Mocninové funkcie sa rozlišujú podľa stupňa mocniny premennej, ktorú obsahujú. Lineárna a konštantná funkcia sú špeciálnym prípadom mocninovej funkcie. Obvykle sa ale v definícii týchto funkcii nepíšu mocniny. V nasledovnej tabuľke sú mocninové funkcie s ich názvami nanajvýš tretieho stupňa:

Stupeň	Predpis funkcie	Názov
$a = - 1$	$f (x) = \frac{n}{x}$	nepriama úmernosť
$a = 0$	$f (x) = n$	konštantná funkcia
$a = 1$	$f (x) = n x$	lineárna funkcia
$a = 2$	$f (x) = n x^{2}$	kvadratická funkcia
$a = 3$	$f (x) = n x^{3}$	kubická funkcia

Vlastnosti mocninových funkcií

Vlastnosti mocninových funkcií sú závislé od stupňa mocniny. Grafy tohto typu funkcií sú rôzne, čo závisí opäť od veľkosti a druhu mocniteľa. Napríklad parabola alebo hyperbola.^[1] Mocninové funkcie s kladným mocniteľom majú tú spoločnú vlastnosť, že všetky prechádzajú začiatkom sústavy súradníc. Ostatné vlastnosti sa navzájom líšia. Keďže vlastnosti závisia od mocniteľa, je lepšie obmedziť sa na funkcie s celočíselným párnym resp. nepárnym mocniteľom.

Funkcia s kladným párnym mocniteľom

$n \in ℝ - {0}, a \in ℤ^{+}$
$f : ℝ \mapsto ℝ; x \mapsto f (x) = n \cdot x^{2 a}$

Vlastnosť	Rozbor	Graf
definičný obor a obor hodnôt	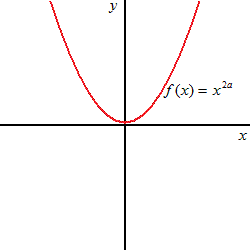$D (f) = ℝ$ $H (f) = ℝ_{0}^{+}$
prostá funkcia	Funkcia nie je prostá, pretože neplatí nasledovná implikácia pre ľubovoľnú dvojicu čísel $[- a; a]$ : $x_{1} \neq x_{2} \Rightarrow n \cdot x_{1}^{2 a} \neq n \cdot x_{2}^{2 a}$
monotónnosť	Ak $n$ je kladné, potom funkcia je klesajúca na intervale $(- \infty; 0)$ a rastúca na intervale $(0; + \infty)$ , v opačnom prípade je funkcia rastúca na intervale $(- \infty; 0)$ a klesajúca na intervale $(0; + \infty)$ .
ohraničenosť, párnosť, nepárnosť	Ak $n$ je kladné, potom je funkcia zdola ohraničená hodnotou 0. V opačnom prípade je zhora ohraničená hodnotou 0. V tejto hodnote nadobúda aj globálny extrém. Funkcia je párna a nie je nepárna, pretože platí $n \cdot (- x)^{2 a} = n \cdot x^{2 a}$
periodická a inverzná funkcia	Funkcia nie je periodická so žiadnou periódou. Funkcia nie je prostá, preto neexistuje inverzná funkcia pre celý definičný obor tejto funkcie. Na podmnožine definičného oboru, na ktorej je prostá existuje inverzná funkcia $f^{- 1} (x) = \sqrt[2 a]{n \cdot x}$
spojitosť a diferencovateľnosť	Funkcia je spojitá a diferencovateľná na celom obore reálnych čísel.

Funkcia s kladným nepárnym mocniteľom

$n \in ℝ - {0}, a \in ℤ_{0}^{+}$
$f : ℝ \mapsto ℝ; x \mapsto f (x) = n \cdot x^{2 a + 1}$

Vlastnosť	Rozbor	Graf
definičný obor a obor hodnôt	$D (f) = ℝ$ $H (f) = ℝ$
prostá funkcia	Funkcia je prostá.
monotónnosť	Ak $n$ je kladné, potom funkcia je rastúca na celom definičnom obore, v opačnom prípade je funkcia klesajúca na celom definičnom obore.
ohraničenosť, párnosť, nepárnosť	Funkcia nie je ohraničená zdola ani zhora. Neexistujú teda ani globálne extrémy. Funkcia je nepárna.
periodická a inverzná funkcia	Funkcia nie je periodická so žiadnou periódou. Funkcia je prostá, preto existuje inverzná funkcia pre celý definičný obor tejto funkcie $f^{- 1} (x) = \sqrt[2 a + 1]{n \cdot x}$
spojitosť a diferencovateľnosť	Funkcia je nespojitá (v bode x=0)

Funkcia so záporným párnym mocniteľom

$n \in ℝ - {0}, a \in ℤ^{+}$
$f : ℝ \mapsto ℝ; x \mapsto f (x) = n \cdot x^{- 2 a}$

Vlastnosť	Rozbor	Graf
definičný obor a obor hodnôt	$D (f) = ℝ - {0}$ $H (f) = ℝ^{+}$
prostá funkcia	Funkcia nie je prostá, pretože neplatí nasledovná implikácia pre ľubovoľnú dvojicu čísel $[- a; a]$ : $x_{1} \neq x_{2} \Rightarrow n \cdot x_{1}^{- 2 a} \neq n \cdot x_{2}^{- 2 a}$
monotónnosť	Ak $n$ je kladné, potom funkcia je rastúca na intervale $(- \infty; 0)$ a klesajúca na intervale $(0; + \infty)$ , v opačnom prípade je funkcia klesajúca na intervale $(- \infty; 0)$ a rastúca na intervale $(0; + \infty)$ .
ohraničenosť, párnosť, nepárnosť	Ak $n$ je kladné, potom je funkcia zdola ohraničená hodnotou 0. V opačnom prípade je zhora ohraničená hodnotou 0. Funkcia je párna a nie je nepárna, pretože platí $n (- x)^{- 2 a} = n \cdot x^{- 2 a}$
periodická a inverzná funkcia	Funkcia nie je periodická so žiadnou periódou. Funkcia nie je prostá, preto neexistuje inverzná funkcia pre celý definičný obor tejto funkcie. Na podmnožine definičného oboru, na ktorej je prostá existuje inverzná funkcia $f^{- 1} (x) = \sqrt[2 a]{\frac{n}{x}}$
spojitosť a diferencovateľnosť	Funkcia nie je spojitá v bode $x = 0$

Funkcia so záporným nepárnym mocniteľom

$n \in ℝ - {0}, a \in ℤ_{0}^{+}$
$f : ℝ \mapsto ℝ; x \mapsto f (x) = n \cdot x^{- 2 a - 1}$

Vlastnosť	Rozbor	Graf
definičný obor a obor hodnôt	$D (f) = ℝ - {0}$ $H (f) = ℝ - {0}$
prostá funkcia	Funkcia je prostá.
monotónnosť	Ak $n$ je kladné, potom funkcia je klesajúca na intervale $(- \infty; 0) \cup (0; + \infty)$ , v opačnom prípade je funkcia na danom intervale rastúca.
ohraničenosť, párnosť, nepárnosť	Funkcia nie je ohraničená zdola ani zhora. Neexistujú teda ani globálne extrémy. Funkcia je nepárna.
periodická a inverzná funkcia	Funkcia nie je periodická so žiadnou periódou. Funkcia je prostá, preto existuje inverzná funkcia pre celý definičný obor tejto funkcie $f^{- 1} (x) = \sqrt[2 a + 1]{\frac{n}{x}}$
spojitosť a diferencovateľnosť	Funkcia nie je spojitá v bode $x = 0$ .

Funkcia má dve asymptoty. Prvá - vodorovná je os $x$ a druhá - zvislá je os $y$

Mocninové funkcie a polynómy

Šablóna:Hlavný článok

Súčtom viacerých mocninových funkcií vznikne polynóm určitého stupňa. Spravidla sa označuje symbolom $P (x)$ , kde $x$ označuje premennú. Stupeň polynómu sa určí podľa najvyššej mocniny, ktorú obsahuje. Polynómy tvoria nadradenú skupinu funkcií k mocninovým, nazvanú polynomické funkcie.

Nech $f_{0}, f_{1}, \dots, f_{k}$ sú mocninové funkcie takého stupňa, aký majú index. Potom zápis

$P (x) = \sum_{i = 0}^{k} a_{i} f_{i} (x)$

kde koeficienty $a_{i}$ sú ľubovoľné reálne čísla, nazývame polynóm $k$ -teho stupňa.^[2]

Mocninové rady

Definícia

Mocninovým radom rozumieme rad funkcií v tvare

$a_{0} + a_{1} x + a_{2} x^{2} + \dots + a_{n} x^{n} + \dots = \sum_{n = 0}^{\infty} a_{n} x^{n}$

respektíve

$a_{0} + a_{1} (x - x_{0}) + a_{2} (x - x_{0})^{2} + \dots + a_{n} (x - x_{0})^{n} + \dots = \sum_{n = 0}^{\infty} a_{n} (x - x_{0})^{n}$

kde $a_{1}, a_{2}, \dots \in ℝ$ .^[3]

Polomer konvergencie mocninového radu

Ak mocninový rad konverguje v bode $x_{0} \neq 0$ , potom absolútne konverguje pre všetky $x \in (- | x_{0} |; | x_{0} |)$ , pričom najväčšiu vzdialenosť bodu $x_{0}$ od počiatku (píšeme $| x_{0} |$ ) nazývame polomerom konvergencie $R$ . Vždy platí, že $R \geq 0$ . K určeniu polomeru konvergencie sa používajú klasické metódy pre konvergenciu nekonečných číselných radov. Ak je polomer konvergencie nenulový, potom je súčet mocninového radu spojitá funkcia v $(- R; R)$ .

Vlastnosti mocninových radov

Ak platí, že pre ľubovoľné $x_{0} \in (- R; R)$ konverguje rad $\sum_{n = 0}^{\infty} a_{n} x^{n}$ , potom taktiež konverguje rad $\sum_{n = 0}^{\infty} (a_{n} x^{n})^{'}$ . Hovoríme, že mocninový rad sa dá derivovať člen po člene.

Taktiež platí, že

\sum_{n = 0}^{\infty} \int_{a}^{b} a_{n} x^{n} = \int_{a}^{b} a_{0} d x + \int_{a}^{b} a_{1} x d x + . . .

na ľubovoľnom intervale $⟨ a; b ⟩ \subset (- R; R)$ a hovoríme, že mocninový rad možno integrovať člen po člene.

Mocninové funkcie a infinitezimálny počet

Šablóna:Hlavný článok

Derivácia mocninovej funkcie je definovaná ako limita
$(n \cdot x^{a})^{'} : = \lim_{h \to 0} \frac{n (x + h)^{a} - n x^{a}}{h}$

Odvodenie derivácie mocninovej funkcie

Všeobecné odvodenie sa uskutoční výpočtom vyššie uvedenej limity

$\begin{matrix} (n x^{a})^{'} : = & \lim \limits_{h \to 0} \frac{n (x + h)^{a} - n \cdot x^{a}}{h} = \lim \limits_{h \to 0} \frac{n \cdot \sum_{i = 0}^{a} (\binom{a}{i}) x^{a - i} \cdot h^{i} - n \cdot x^{a}}{h} = \lim \limits_{h \to 0} \frac{n \cdot (x^{a} + a \cdot x^{a - 1} h + \dots + h^{a}) - n \cdot x^{a}}{h} = \\ = & \lim \limits_{h \to 0} \frac{h \cdot (n \cdot a \cdot x^{a - 1} + \dots + n \cdot h^{a - 1})}{h} = n \cdot a \cdot x^{a - 1} \end{matrix}$

Primitívna funkcia k mocninovej funkcii

Šablóna:Hlavný článok Pre mocninové funkcie platí

$F (x) = n \int x^{a} d x = \frac{n \cdot x^{a + 1}}{a + 1} + C; a \neq - 1$

Tento integrál sa nazýva aj tabuľkový integrál. Primitívna funkcia k mocninovej funkcii je od nej o jeden stupeň vyššia (hodnota mocniny sa zvýši o jeden stupeň). To znamená, že primitívna funkcia k lineárnej je kvadratická, ku kvadratickej je kubická atď. Špeciálnym prípadom je nepriama úmernosť, kde primitívna funkcia vyzerá nasledovne
$F (x) = n \int \frac{1}{x} d x = {\ln | x |}^{n} + C; x \neq 0$

Určitý integrál mocninovej funkcie

Šablóna:Hlavný článok Nech $U = ⟨ α; β ⟩$ . Potom určitým integrálom mocninovej funkcie rozumieme číslo

$n \int_{U} x^{a} d x = \frac{n (β^{a + 1} - α^{a + 1})}{a + 1}$

V prípade nepriamej úmernosti

$n \int_{U} \frac{1}{x} d x = \ln {| \frac{β}{α} |}^{n}$

Aplikácie mocninových funkcií

Pomocou mocninových funkcií je možné modelovať rôzne jednoduché situácie z bežného života. Príkladom môžu byť ekonomické aplikácie, fyzikálne aplikácie i aplikácie priamo v matematike.

Aplikácie vo fyzike

Jednoduchou, ale významnou fyzikálnou aplikáciou mocninových funkcií je opis dráhy telesa pri voľnom páde. Tento jav popisuje funkcia

$s (t) = \frac{1}{2} g t^{2}; t \geq 0$

kde $g$ je gravitačná konštanta. Podľa druhu mocninovej funkcie ide o kvadratickú funkciu, kde ako premenná vystupuje čas - $t$ .^[4]

Aplikácie v matematike

V matematike by sa dala aplikácia hľadať pri výpočtoch obsahov a objemov. Aby vznikla funkcia jednej premennej, je možné opísať závislosť obsahu štvorca od veľkosti jeho strany. Tento jav sa dá popísať funkciou obsahu štvorca

$S (a) = a^{2}; a \geq 0$

Ide o kvadratickú funkciu, kde premenná je $a$ a vyjadruje dĺžku strany štvorca. Iný príklad by bol na výpočet obsahu rovnoramenného pravouhlého trojuholníka. Táto funkcia je

$S (v) = \frac{1}{2} v^{2}; v \geq 0$

Aplikácia kubickej funkcie by sa dala hľadať pri výpočte objemu kocky a táto funkcia potom vyzerá nasledovne

$V (a) = a^{3}; a \geq 0$

Podobne ako pri trojuholníku, z funkcie objemu kocky by sa dala vyjadriť funkcia objemu ihlana. Zovšeobecnením predchádzajúceho je možné zistiť, že všetky matematické vzorce pre výpočet nejakej kvantity, sú závislé od hodnôt, ktoré do vzťahu dosadzujeme. Všetky tieto predpisy sú teda funkcie a hodnoty, ktoré sa do nich dosadzujú, sú chápané ako premenné.
Aplikácie nepriamej úmernosti možno hľadať v praktických situáciách. Nepriama úmernosť vyjadruje taký vzťah dvoch veličín, že nárast jednej spôsobí pokles druhej a opačne. Všeobecne sa problémové úlohy nepriamej úmernosti riešia cez tzv. trojčlenku. Jednoduchý príklad objasňuje základný princíp nepriamej úmernosti: Auto prejde pri rýchlosti Šablóna:Km/h určitú vzdialenosť za 30 minút. Ako dlho by autu trvala rovnaká cesta, ale pri rýchlosti Šablóna:Km/h? Zostavením trojčlenky

$↑ \begin{matrix} 100 & \dots & 30 \\ 120 & \dots & y \\ 120 : 100 & = & 30 : y \end{matrix} ↓$

Výpočtom danej rovnice dostávame výsledok, že auto prejde pri rýchlosti Šablóna:Km/h danú vzdialenosť za 25 minút. Na trojčlenku sa dá pozrieť aj všeobecnejšie. Ak by sme potrebovali opakovať ten istý algoritmus s inou rýchlosťou, potom treba zopakovať celý výpočet trojčlenky. Jednoduchým odvodením všeobecného vzťahu je možné vyhnúť sa počítaniu cez trojčlenku a chápať zápis ako funkciu:

$↑ \begin{matrix} 100 & \dots & 30 \\ x & \dots & f (x) \\ x : 100 & = & 30 : f (x) \end{matrix} ↓$

Úpravami získame funkciu

$f (x) = \frac{3000}{x}$

kde za premennú $x$ dosadzujeme konkrétnu rýchlosť a získame tak hodnotu $f (x)$ , ktorá vyjadruje počítaný čas. Z matematického hľadiska ide o mocninovú funkciu - nepriamu úmernosť a číslo 3000 nazýva koeficient nepriamej úmernosti $k$ .

Referencie

Šablóna:Referencie

Pozri aj

Iné projekty

Šablóna:Projekt

Externé odkazy

Zdroj

Šablóna:Citácia knihy

↑ Kadlečková, M, Zimka, R: Matematika, Mat-Centrum, 1997
↑ Kolek, L: Přehled vzorců středoškolské matematiky, str. 98, Polytechnická knižnice, 1970
↑ Kolek, L: Přehled vzorců středoškolské matematiky, str. 222, Polytechnická knižnice, 1970
↑ Mikulčák, J a kol.: Matematické fyzikálne a chemické tabuľky, SPN, 2002

[1] Kadlečková, M, Zimka, R: Matematika, Mat-Centrum, 1997

[2] Kolek, L: Přehled vzorců středoškolské matematiky, str. 98, Polytechnická knižnice, 1970

[3] Kolek, L: Přehled vzorců středoškolské matematiky, str. 222, Polytechnická knižnice, 1970

[4] Mikulčák, J a kol.: Matematické fyzikálne a chemické tabuľky, SPN, 2002

[1]

[2]

[3]

[4]

Mocninová funkcia

Obsah

Definícia

Druhy mocninových funkcií