Množina

Množina je súhrn dobre rozlíšiteľných entít, ktorý chápeme ako celok. Presnejšie definície sa rôznia. Množinami sa zaoberá teória množín.

Algebrické množiny označujeme veľkými písmenami latinskej abecedy. Entity, ktoré množina obsahuje sa nazývajú prvky množiny. Označujeme ich malými písmenami latinskej abecedy.

$A=\{c,f,h,j\}$

Každá množina má svoju mohutnosť (kardinalitu), čo je zovšeobecnenie pojmu počet prvkov množiny. Napríklad mohutnosť množiny $M=\{a,b,c,d\}$ je $4$. Mohutnosť množiny sa zvyčajne označuje $|M|$. Mohutnosť prázdnej množiny je 0.

Triedenie množín

Podľa vlastností, ktorými disponuje konkrétna množina poznáme:

• prázdna množina, ktorá neobsahuje žiaden prvok a označuje sa $M=\{\}$ alebo $M=\varnothing$, ale nikdy nie $M=\{\varnothing \}$ pretože takýto zápis naznačuje, že množina $M$ obsahuje jednu prázdnu množinu $\varnothing$ a teda $M$ už nemôže byť prázdna množina,
• neprázdna množina, ktorá obsahuje aspoň jeden prvok, napríklad $M=\{a,b,c\}$, platí $M\ne \varnothing$,
• jednoprvková množina, zriedkavejšie označovaná aj ako singleton, obsahuje len jeden prvok, pri určovaní takejto množiny sa niekedy neuvádzajú zložené zátvorky, takéto značenie sa však nedoporučuje, napr. $M=\{a\}=a$,
• neusporiadaná množina, v ktorej na poradí jednotlivých prvkov množiny nezáleží,
• usporiadaná množina, v ktorej záleží na poradí prvkov, takéto množiny sa používajú hlavne v štatistike, geodézii, ekonómii a pod.,
• konečná množina, pri ktorých sa dá vyjadriť počet ich prvkov, napríklad počet obyvateľov vo všetkých okresných SR, medzi konečné množiny patrí aj prázdna množina pretože počet jej prvkov je rovný nule takže sa dá vyjadriť,
• nekonečná množina, ktorá obsahuje nekonečný počet prvkov, napr. $\mathbb{N}$, $\mathbb{Z}$ alebo $ℝ$,
• spočítateľná (nekonečná) množina, ktorá obsahuje prvky, ktoré sa dajú spočítať, napr. $\mathbb{N}$ alebo $\mathbb{Z}$,
• nespočítateľná (nekonečná) množina, ktorej prvky sa nedajú spočítať, napr. $ℝ$.
• potenčná množina alebo potenčný systém množiny je v matematike množina všetkých podmnožín množiny M a označuje sa $𝒫(M)$ alebo $2^M$. Napríklad všetky podmnožiny množiny $M=\{a,b\}$ sú $M_1=\{\}$ (prázdna množina je vždy podmnožinou každej množiny), $M_2=\{a\}$, $M_3=\{b\}$ a $M_4=\{a,b\}$. Počet všetkých podmnožín každej množiny $M$ je $2^n$ kde $n$ je počet prvkov v množine.

Určenie množín

Prvky množiny sa určujú nasledovnými spôsobmi:

Vymenovaním všetkých prvkov, napríklad $M=\{1,2,3,4,5,6,7,8,9,0,a,b,c,d,e,f\}$ (všetky cifry používané v zápise šestnástkovej číselnej sústavy). Pri takomto určovaní, ak sú z kontextu jednoznačne známe všetky prvky množiny, je možné použiť aj skrátený spôsob $M=\{1,2,3,\dots ,d,e,f\}$.

Určením vlastností, ktorými bez výnimky disponujú všetky prvky množiny. Napríklad $M=\{x\in \mathbb{N},5\le x\le 26\}$ pre všetky prirodzené čísla väčšie alebo rovné 5 a zároveň menšie alebo rovné 26.

Kombináciou vymenovania a určenia vlastností. Napr. $M=\{x\in \mathbb{N}+\{\pi ,e,\phi ,i\}\}$ je množina všetkých prirodzených čísel a štyroch matematických konštánt.

Dedičnosťou respektíve kombináciou určení, ktorá vzniká pri množinových operáciách. Napríklad

$\begin{array}{cc}A& =\{5,6,7,8,9,10,11,12,13\}=\{x\in \mathbb{N},5\le x\le 13\}\\ B& =\{3,6,9,12,15\}=\{x\in \mathbb{N},3|x\wedge x<16\}\\ A\cup B& =\{6,9,12\}=\{x\in \mathbb{N},5\le x\le 13,3|x\wedge x<16\}=\{x\in \mathbb{N},6\le x\le 12,3|x\}\\ \end{array}$.

Niektoré množiny čísel majú v matematike svoje ustálené značenia:

• $\mathbb{N}=\{1,2,3,\dots \}$ je množina prirodzených čísel.
  • Pre množinu čísel $\mathbb{N}+\{0\}$ sa niekedy používa označenie ${\mathbb{N}}^0$, ${\mathbb{N}}^{+}$ alebo ${\mathbb{N}}^{+0}$, v tomto značení exponent neznamená mocninu. Tiež je možné sa stretnúť s označením $𝕎$ (z anglického whole).
• $\mathbb{Z}=\{\dots ,-2,-1,0,1,2,\dots \}$ je množina celých čísel.
  • Pre množinu čísel $\mathbb{Z}-\{0\}$ sa niekedy používa označenie ${\mathbb{Z}}^{-0}$, v tomto značení exponent neznamená mocninu.
• $\mathbb{Q}$ je množina racionálnych čísel (patria sem zlomky).
• $𝕀$ alebo $ℝ\setminus \mathbb{Q}$ je množina iracionálnych čísel (napr. niektoré odmocniny, π).
• $𝔸$ je množina všetkých algebraických čísel.
• ${𝔸}_R$ je množina reálnych algebraických čísel.
• $ℝ$ je množina reálnych čísel.
• $ℂ$ je množina komplexných čísel (napr. odmocniny záporných čísel).
• $ℍ$ sú kvaterniony (hyperkomplexné čísla).
• $𝕆$ sú oktoniany (hyperkomplexné čísla).
• $𝕊$ sú sedeniony (hyperkomplexné čísla).
• $𝕋$ sú trigintaduoniny (hyperkomplexné čísla).
• $\mathbb{P}$ je množina všetkých prvočísel.

Množinové vzťahu uvedených množín čísel je možné vyjadriť napríklad zápisom:

$\mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q}\subset ℝ\subset ℂ$.

Vzťahy medzi množinami

Základné vzťahy medzi dvoma (alebo viacerými) množinami sú

značenie	(definícia a) popis	príklad
$A=B$	Rovnosť množín $A$ a $B$.	$\{a,b,c\}=\{a,b,c\}$
$A\ne B$	Nerovnosť množín $A$ a $B$.	$\{a,b,c\}\ne \{d,e,f\}$
$A\subset B$	$\mathrm{\forall }x(x\in A⟹x\in B)$ Množina $A$ je vlastná podmnožina množiny $B$.	$\{a,b,c\}\subset \{a,b,c\}$
$A\subseteq B$	$\mathrm{\forall }x(x\in A⟹x\in B)\wedge \mathrm{\exists }x(x\in B\wedge x\in ̸A)$ Množina $A$ je podmnožina množiny $B$.	$\{a,b\}\subseteq \{a,b,c\}$
$A\subset ̸B$	Množina $A$ nie je vlastná podmnožina množiny $B$.	$\{a,b\}\subset ̸\{a,b,c\}$
$A\subseteq ̸B$	Množina $A$ nie je podmnožina množiny $B$.	$\{d,e\}\subseteq ̸\{a,b,c\}$

UPOZORNENIE. Pri učovaní vzťahov medzi dvoma množinami panuje nekonzistentnosť prameniaca z historického vývoja. V minulosti (v staršom systéme) sa symboly $\subset$ a $\supset$ používali pre vzťah s akoukoľvek podmnožinu/nadmnožinu množiny a symboly $⊊$ a $⊋$ sa používali pre vzťah s vlastnou podmnožinou/nadmnožinou množiny. V novšom systéme sa symboly $\subset$ a $\supset$ používajú pre vyjadrenie vzťahu s vlastnou podmnožinou (tzv. ostrá inklúzia) a pre obecné podmnožiny sa používajú znaky $\subseteq$ a $\supseteq$ (istá analógia so symbolmi $\le$ a $\ge$). Vo vyššie uvedenej tabuľke je použitá novší systém značenia.

Grafické znázornenie množín

• Oválový diagram – znázornenie množiny pomocou uzavretej čiary, pričom prvky patriace množine znázorníme bodmi vnútri oválu a prvky nepatriace množine bodmi mimo oválu
• Vennov diagram – U je množina obsahujúca všetky prvky, ktoré uvažujeme

Množinové operácie

Karteziánsky súčin

Karteziánsky súčin množiny $A$ a množiny $B$ je množina všetkých usporiadaných dvojíc $(a,b)$, kde prvky $a$ sú prvky z množiny $A$ a prvky $b$ sú prvky z množiny $B$. Karteziánsky súčin množín $A$ a $B$ sa bežne označuje znakom $A\times B$. Formálne sa Karteziánsky súčin definuje vzťahom

$A\times B\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\{(a,b)|a\in A\wedge b\in B\}$.

Napríklad

$\begin{array}{cc}A& =\{a,b,c\}\\ B& =\{\alpha ,\beta \}\\ A\times B& =\{a,b,c\}\times \{\alpha ,\beta \}\\ & =\{(a,\alpha ),(a,\beta ),(b,\alpha ),(b,\beta ),(c,\alpha ),(c,\beta )\}\\ \end{array}$,

ale

$\begin{array}{cc}A& =\{a,b,c\}\\ B& =\{\alpha ,\beta \}\\ B\times A& =\{\alpha ,\beta \}\times \{a,b,c\}\\ & =\{(\alpha ,a),(\alpha ,b),(\alpha ,c),(\beta ,a),(\beta ,b),(\beta ,c)\}\\ \end{array}$..

Karteziánsky súčin teda nie je komutatívna a nie je ani asociatívna množinová operácia.

Zjednotenie

Zjednotenie množín A a B je množina všetkých prvkov z množiny U, ktoré patria aspoň do jednej z množín A a B (A U B)

Pre viac informácií o zjednotení množín, pozrite článok Zjednotenie.

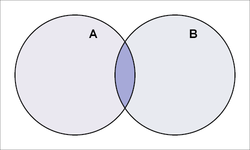
Prienik

Prienik množín A a B je množina všetkých prvkov, ktoré patria do množiny A a zároveň do množiny B (A ∩ B)

Pre viac informácií o prieniku množín, pozrite článok Prienik.

Rozdiel

Rozdiel množín A a B je množina všetkých prvkov, ktoré patria množine A, ale nepatria množine B (A – B)

Pre viac informácií o rozdiele množín, pozrite článok Rozdiel množín.

Doplnok (komplement)

Doplnok (komplement) množiny $A$ je množina všetkých prvkov patriacich množine $U$, ktoré nepatria množine $A$, označuje sa $A^{\prime }=U-A$

Pre viac informácií o doplnku množiny, pozrite článok Doplnok.

Externé odkazy

• Množina na pohodovamatematika.sk