Mnohouholník

Mnohouholník alebo polygón alebo n-uholník je časť roviny vymedzená úsečkami, ktoré spájajú určitý počet bodov (najmenej tri), z ktorých žiadne tri susedné neležia na jednej priamke. Inak povedané: mnohouholník je obmedzená časť roviny ohraničená uzatvorenou lomenou čiarou.

Všeobecne

Body, ktoré určujú mnohouholník, sa nazývajú vrcholy mnohouholníka. Úsečky, ktoré spájajú susedné vrcholy, sa nazývajú strany mnohouholníka. Úsečky, ktoré spájajú nesusedné vrcholy, sa nazývajú uhlopriečky. Uhly, ktoré zvierajú susedné strany, sa nazývajú vnútorné uhly mnohouholníka. Počet vrcholov, strán a vnútorných uhlov v jednom mnohouholníku je rovnaký a tento počet určuje názov mnohouholníka: trojuholník, štvoruholník, päťuholník atď.

Znázornenie

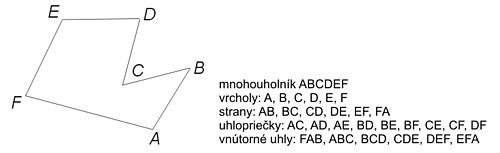
Mnohouholník sa znázorňuje pomocou jeho vrcholov a strán, označuje sa vymenovaním vrcholov v ich presnom poradí. Pri špeciálnych mnohouholníkoch (trojuholník, štvorec, obdĺžnik a pod.) sa v zápise pred vymenovaním vrcholov umiestňuje príslušný symbol (Δ a pod.). Vrcholy, strany a uhly mnohouholníka sa zapisujú rovnakým spôsobom ako body, úsečky a uhly.

Znázornenie mnohouholníka

Druhy mnohouholníkov

Okrem mnohouholníkov líšiacich sa počtom vrcholov, sa mnohouholníky delia na:

• pravidelné (všetky strany a vnútorné uhly sú zhodné) a nepravidelné.
• konvexné (všetky vnútorné uhly sú menšie ako 180°) a nekonvexné (aspoň jeden vnútorný uhol je väčší ako 180°)

Vlastnosti

Obvod mnohouholníka $o$ sa vypočíta ako súčet všetkých jeho strán: $o=a+b+c+...$, kde $a,b,c,...$ sú jednotlivé strany mnohouholníka.

Obsah všeobecného mnohouholníka $S$ sa vypočíta pomocou rozloženia mnohouholníka na vhodné vzájomne sa neprekrývajúce trojuholníky, obdĺžniky alebo štvorce, ktorých obsahy $S_1,S_2,...$ sa vypočítajú podľa známych vzorcov a následne sa spočítajú: $S=S_1+S_2+...$

Súčet vnútorných uhlov mnohouholníka je rovný $\pi (n-2)\mathrm{r}\mathrm{a}\mathrm{d}$

Počet uhlopriečok všeobecného $n$-úholníka určíme zo vzťahu $\frac{1}{2}n(n-3)$

Ak existuje taká kružnica, že na nej ležia všetky vrcholy daného mnohouholníka, potom hovoríme, že je mnohouholníku opísaná. Mnohouholník, ktorému je možné opísať kružnicu sa nazýva tetivový (jeho strany sú tetivami opísanej kružnice).

Súčet uhlov všetkých trojuholníkov n uholníka dotýkajucich sa jeho stredu sa rovná 360°.

Vlastnosti pravidelného mnohouholníka

Veľkosť vnútorného uhla pravidelného $n$-uholníka má hodnotu ${\alpha }_n=\frac{n-2}{n}\pi$

Veľkosť stredového, resp. vonkajšieho uhla je rovná ${\alpha }_n^{\prime }=\frac{2\pi }{n}$

Pravidelnému mnohouholníku je možné opísať a zároveň vpísať kružnicu. Stredy oboch kružníc ležia v rovnakom bode, ktorý je totožný s ťažiskom mnohouholníka.

Ak označíme dĺžku strany pravidelného $n$-uholníka ako $a_n$ a polomer opísanej kružnice ako $r_n$, potom polomer ${\rho }_n$ vpísanej kružnice je možné určiť zo vzťahu ${\rho }_n=\frac{1}{2}\sqrt{4r_n^2-a_n^2}$

Vpísaný a opísaný pravidelný n-uholník

Z obrázka vidno, že existujú dva druhy n-uholníka:

Vpísaný n-uholník

Pre vpísaný polygón platí:

v=|KW|

r=|KV|

$S_n=\frac{n{r}^2\sin \alpha }{2}$

Opísaný n-uholník

Pre opísaný polygón platí:

R=|KL|

r=|KV|

$S_N=n{R}^2\tan \frac{\alpha }{2}$

Pozri aj

• Planimetria
• Mnohosten