Morfologické operácie

Morfologické operácie (Šablóna:Vjz) sú jedny z techník spracovania obrazu v informatike. Používajú sa hlavne pri predspracovaní obrázkov na odstránenie šumu a zjednodušenie tvaru, ďalej môžu byť použité na tvorbu kostry alebo stenčovanie a zhrubšovanie objektov. Najčastejšie sú používané na binárne obrazy, avšak je možné použiť ich aj na šedotónové. Medzi základné morfologické operácie patrí dilatácia, erózia a od nich odvodené otvorenie a uzavretie.

Definícia

Príklady štrukturálnych elementov

Morfologické operácie sú realizované ako relácie bodovej množiny – vstupného obrazu a menšej bodovej množiny nazývanej štrukturálny element. Štrukturálny element B je systematicky posúvaný po obraze a výsledok transformácie je zapisovaný do výsledného obrázku.

Štrukturálny element je matica, ktorej rozmer je zvyčajne nepárne číslo. Je to z toho dôvodu aby pixel z pôvodného obrázku po ktorom maticu posúvame, padol do jej stredu. Binárny štrukturálny element pozostáva z jednotiek a núl. V niektorých reprezentáciách môžeme nájsť zapísané len jednotky.

Dilatácia

Dilatácia $\oplus$ rozširuje objekty o jednu vrstvu na úkor pozadia a spája rozdelené časti objektu. Používa sa taktiež na vyplnenie drobných dier a úzkych zálivov.

Majme vstupný obraz X a štrukturálny element B. Dilatácia potom skladá body týchto dvoch množín na základe vektorového súčtu (alebo aj Minkowskeho súčtu, čo je (a,b) + (c,d) = (a+c, b+d)). Dilatácia X $\oplus$ B je množina bodov, ktorá je výsledkom všetkých možných súčtov párov vektorov, pričom pár tvorí stále jeden vektor z množiny X a druhý z množiny B. Formálne zapísané:

$X\oplus B=\{p\in {\epsilon }^2:p=x+b,x\in X\text{ a }b\in B\}$

Nasledujúci príklad ukazuje ako zo vstupného obrazu X a štrukturálneho elementu B vypočítať obraz po dilatácii:

X = {(1,0),(1,1),(1,2),(2,2),(0,3),(0,4)}

B = {(0,0),(1,0)}

X ⊕ B = {(1,0),(1,1),(1,2),(2,2),(0,3),(0,4),(2,0),(2,1),(2,2),(3,2),(1,3),(1,4)}

Použitie morfologických operácii: (a) pôvodný obrázok, (b) dilatácia a (c) erózia.

Erózia

Erózia ⊖ skladá body dvoch množín na základe vektorového rozdielu. Eliminuje izolované body na pozadí, uberá hrúbku objektov a zložité objekty rozdeľuje. Eróziu X⊖B môžeme vyjadriť rovnicou:

$X\ominus B=\{p\in {\epsilon }^2:p+b\in X\text{ pre každé }b\in B\}$

Pričom táto rovnica nám hovorí, že každý bod p z obrázku je testovaný a výsledok erózie je daný takými bodmi p, ktorých vektorový súčet p+b patrí do X.

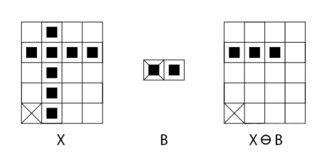
Nasledujúci príklad ukazuje ako zo vstupného obrazu X a štrukturálneho elementu B vypočítať obraz po erózii:

X = {(1,0),(1,1),(1,2),(0,3),(1,3),(2,3),(3,3),(1,4)}

B = {(0,0),(1,0)}

X ⊕ B = {(0,3),(1,3),(2,3)}

Otvorenie

Otvorenie (rovnako aj uzavretie) využíva vzájomnú kombináciu morfologický operácii dilatácie a erózie. Využíva sa tu skutočnosť že tieto operácie nie sú navzájom inverznými operáciami. Otvorenie je erózia nasledovaná dilatáciou. Táto operácia prerušuje tenké spoje medzi objektami a odstraňuje šum. Otvorenie je definované ako:

Použitie morfologických operácii: (a) pôvodný obrázok, (b) otvorenie a (c) uzavretie.

$X\circ B=(X\ominus B)\oplus B$

Uzavretie

Uzavretie je dilatácia nasledovaná eróziou. Spája objekty, ktoré sú blízko u seba, zaplňuje malé diery v objektoch a vyhladzuje ich obrysy. Uzavretie je definované ako:

$X\bullet B=(X\oplus B)\ominus B$