Adiabatický dej

Adiabatický dej alebo adiabatický proces je termodynamický dej, pri ktorom nedochádza k tepelnej výmene medzi látkou a okolím.

Pokiaľ je adiabatický proces zároveň vratný, menia sa počas neho iba tlak, objem a teplota plynu, nemení sa jeho entropia. Adiabatický vratný dej sa nazýva aj izoentropický. Nie každý adiabatický proces je teda izoentropický. Adiabatické vratné procesy v prírode neexistujú ani sa nedajú realizovať v technických zariadeniach. Slúžia však ako teoretické modely a definujú cieľový stav, ku ktorým sa snažia technické zariadenia priblížiť. Pomocou nich sa definuje aj adiabatická účinnosť zariadení.

Nevratné adiabatické procesy

Podmienku, aby nedochádzalo k tepelnej výmene medzi pracovnou látkou a okolím s prijateľným priblížením spĺňa väčšina zariadení, ktoré pracujú dostatočne rýchlo aby nebol dostatok času na prestup tepla medzi systémom a okolím. Príkladom takýchto procesov sú adiabatické prúdenie v dýzach alebo lopatkových mrežiach turbín, prúdenie cez prekážky - škrtenie. Prestup tepla je taký malý, že ho možno pre technické výpočty zanedbať. Prejavujú sa ale vnútorné nevratnosti v systéme, ktoré spôsobia zmenu teploty na úkor energie prúdenia. V niektorých zariadeniach nie je ani toto zjednodušenie prípustné a zmeny prebiehajú polytropicky.

S adiabatickými procesmi v reálnych zariadeniach súvisí aj ich tzv. adiabatizácia. Ide o používanie materiálov, ktoré znižujú prestup tepla z pracovnej látky do okolia a tým proces približujú k cieľovému adiabatickému bez prestupu tepla. Príkladom je používanie keramických povlakov pre exponované časti spaľovacieho priestoru spaľovacích motorov.

Vratné adiabatické procesy

Vratné adiabatické procesy sú teoretickým modelom. Ťažšie ako podmienku tepelnej izolácie od okolia je dodržať podmienky vratnosti.

Vratný adiabatický dej ideálneho plynu

Pre adiabatický dej s ideálnym plynom platí Poissonov zákon:

• $p{V}^{\kappa }=\text{const.}$
• $T{V}^{\kappa -1}=\text{const.}$
• $T{p}^{\frac{1-\kappa }{\kappa }}=\text{const.}$

Exponent $\kappa$ sa nazýva Poissonova konštanta a nadobúda hodnoty:

• pre jednoatómový reálny plyn $\kappa \approx 1,67$
• pre dvojatómové plyny $\kappa \approx 1,40$
• pre trojatómové plyny $\kappa \approx 1,33$

Adiabatická zmena teploty

Pri zmene tlaku v plyne (napríklad pri stlačení piestu), bez výmeny tepla so stenami nádoby a iných dejov (vyparovanie/kondenzácia, horenie a pod.), príde ku adiabatickej zmene teploty, ktorú môžme odvodiť z Poissonovho zákona.

$T_1=T_0.{\left(\frac{p_0}{p_1}\right)}^{\frac{1-\kappa }{\kappa }}$

kde:

• T₀ a p₀ sú východiskové podmienky
• T₁ je teplota pri tlaku p₁

Vratná adiabata (izoentropa)

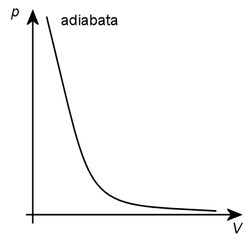
Závislosť tlaku na objeme plynu pri priebehu adiabatického deja graficky vyjadruje krivka adiabata:

Môžu pri ňom nastať dva deje:

• 1. Adiabatická kompresia
• 2. Adiabatická expanzia

Pretože pri adiabatickom deji nedochádza k výmene tepla s okolím, bude $\delta Q=0$. Podľa prvého termodynamického zákona potom platí vzťah

$\mathrm{d}U=\delta W$

To sa dá interpretovať tak, že pri adiabatickom stláčaní ($\mathrm{d}V<0$) plyn prácu prijme a dôjde tak ku rastu vnútornej energie ($\mathrm{d}U>0$), čím sa plyn ohreje. Pri rozpínaní ($\mathrm{d}V>0$) plyn naopak koná prácu na úkor vnútornej energie ($\mathrm{d}U<0$), čím sa ochladzuje. Celková zmena vnútornej energie je teda rovná vykonanej práci $W$.

Podľa stavovej rovnice ideálneho plynu (ak $p\mathrm{d}V+V\mathrm{d}p=nR\mathrm{d}T$) je možné napísať

$\mathrm{d}Q=n{C}_V\mathrm{d}T+p\mathrm{d}V=\frac{C_V}{R}(p\mathrm{d}V+V\mathrm{d}p)+p\mathrm{d}V=0$

Využitím Mayerovej rovnice a po vydelení $pV$ dostaneme

$C_V\frac{\mathrm{d}p}{p}+C_p\frac{\mathrm{d}V}{V}=0$

S využitím Poissonovej konštanty je možné predchádzajúce zapísať ako

$\frac{\mathrm{d}p}{p}+\kappa \frac{\mathrm{d}V}{V}=0$

odkiaľ po integrácii dostaneme

$\ln p+\ln V^{\kappa }=\text{konst}$

a po odlogaritmovaní

$p{V}^{\kappa }=\text{konst}$

Energetická bilancia

Pri adiabatickom deji sa práca koná na úkor vnútornej energie. Pre celkovú prácu teda bude platiť

$W=\int \mathrm{d}U=\int n{C}_V\mathrm{d}T=n{C}_V(T_2-T_1)$

Z Mayerovej rovnice s pomocou Poissonovej konštanty je možné prácu vyjadriť v tvare

$W=n\frac{R}{\kappa -1}(T_2-T_1)$

Z tejto rovnice je možné s pomocou stavovej rovnice vylúčiť teplotu, tzn. $T=\frac{pV}{nR}$, čím dostaneme

$W=\frac{p_2{V}_2-p_1{V}_1}{\kappa -1}$

Ako už bolo povedané pri adiabatickom deji plyn koná prácu W na úkor svojej vnútornej energie ΔU, alebo opačne, práca W vykonaná na plyne spôsobí zvýšenie vnútornej energie ΔU plynu.

Z 1. termodynamického zákona vyplýva ΔU = W. Pre prácu vykonanú plynom medzi bodmi 1 a 2 platí:

$W=\frac{1}{\kappa -1}.(p_2.V_2-p_1.V_1)$

• κ - Poissonova konštanta
• p₁ - tlak plynu v stave 1
• V₁ - objem plynu v stave 1
• p₂ - tlak plynu v stave 2
• V₂ - objem plynu v stave 2

Aby plyn nemohol vymeniť žiadne teplo s okolím, mal by adiabatický dej prebiehať v dokonale izolovanom prostredí, alebo nekonečne rýchlo.

Pre entropiu pri adiabatickom deji platí

$\mathrm{d}S=\frac{\mathrm{d}Q}{T}=0$