Priestorový uhol

Vymedzenie priestorového uhla na guľovej ploche

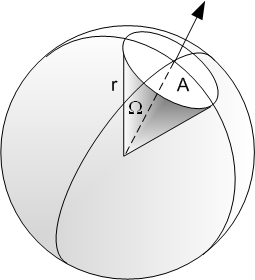
Priestorový uhol je časť priestoru vymedzená rotačnou kužeľovou plochou. Každá taká plocha delí priestor na práve dve časti – priestorové uhly. Priestorový uhol sa určuje tak, že sa uvažuje guľová plocha so stredom vo vrchole V a s ľubovoľným polomerom r, ktorej prienik s priestorovým uhlom je vrchlík na guľovej ploche s obsahom A. Veľkosť priestorového uhla potom určuje pomer medzi A a r², pričom nezávisí na uvažovanej guľovej ploche.

Alternatívnou definíciou priestorového úhlu je zjednotenie všetkých polopriamok $\overrightarrow{VX}$ so spoločným začiatkom V, kde bod X leží na guľovom vrchlíku so stredom v bode V.

Špecifickým prípadom priestorového uhla je polpriestor, tj. časť priestoru rozdeleného rovinou.

Značenie

• Symbol veličiny: $\mathrm{\Omega }$
• Jednotka SI: steradián, značka jednotky: sr
• V astronómii sa okrem steradiánu používa aj staršia jednotka štvorcový stupeň.

Výpočet

Priestorový uhol objektu pozorovaného z určitého bodu je rovný ploche, ktorú zaberá obraz tohto objektu v bodovej projekcii (so stredom v danom bode) na jednotkovú guľu, ktorá má stred v danom bode.

Plný priestorový uhol má hodnotu $4\pi$, priamy uhol polovičnú.

Element priestorového uhla

Ak pozorujeme z určitého bodu s polohovým vektorom $𝐫$ element plochy $\mathrm{d}𝐒$, ktorého polohový vektor je ${𝐫}^{\prime }$, potom pre element priestorového uhla platí

$\mathrm{d}\mathrm{\Omega }=\frac{𝐑\cdot \mathrm{d}𝐒}{R^3}$,

kde $𝐑=𝐫-{𝐫}^{\prime }$, $R$ je veľkosť tohto vektoru a $\mathrm{d}𝐒=𝐧\mathrm{d}S$, pričom $𝐧$ je normála plochy v bode ${𝐫}^{\prime }$.

Pozri aj

• Uhol
• Steradián